§在无向图中
Tarjan 可以求割点/桥,求点双/边双。
我们将图中的边分为「树边」和「非树边」。
定义 $dfn[i]$ 为到达 $i$ 的时间戳,$low[x]$ 表示以 $x$ 为根的子树中所有点只走一条边非树边能到达的最小时间。
无向图中求 $dfn$ 和 $low$ 的代码:
1
2
3
4
5
6
7
8
9
10
11
|
int dfn[N], low[N], Time;
void dfs(int x, int frm) {
dfn[x] = low[x] = ++Time;
for (node i : edge[x]) {
if (!dfn[i.to]) {
dfs(i.to, i.num);
low[x] = min(low[x], low[i.to]);
} else if (i.num != frm)
low[x] = min(low[x], dfn[i.to]);
}
}
|
如果一个点儿子的 $low[to]>dfn[x]$ ,就可以说明 $x\to to$ 的边为割边。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
#include <bits/stdc++.h>
#define pii pair<int, int>
using namespace std;
const int N = 160;
struct node {int to, num;};
vector<node> edge[N];
vector<pii> ans;
int dfn[N], low[N], n, m, cnt, Time;
void dfs(int x, int frm) {
dfn[x] = low[x] = ++Time;
for (node i : edge[x]) {
if (!dfn[i.to]) {
dfs(i.to, i.num);
low[x] = min(low[x], low[i.to]);
if (low[i.to] > dfn[x])
ans.push_back({ x, i.to });
} else if (i.num != frm)
low[x] = min(low[x], dfn[i.to]);
}
}
int main() {
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int x, y;
cin >> x >> y;
edge[x].push_back({ y, ++cnt });//将边编号
edge[y].push_back({ x, cnt });
}
dfs(1, 0);
sort(ans.begin(), ans.end());
for (pii i : ans) cout << i.first << " " << i.second << '\n';
}
|
先求出割边并标记,然后不经过割边跑DFS即可。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+100;
int dfn[N],low[N],n,m,cnt,Time,mark[N*10],col,vis[N];
struct node{int to,num;};
vector<node>edge[N];
vector<int>ans[N];
void tarjan(int x,int frm){
dfn[x]=low[x]=++Time;
for(node i:edge[x]){
if(!dfn[i.to]){
tarjan(i.to,i.num);
low[x]=min(low[x],low[i.to]);
if(low[i.to]>dfn[x]) mark[i.num]=1;
}else if(i.num!=frm) low[x]=min(low[x],dfn[i.to]);
}
}
void dfs(int x){
if(vis[x]) return;
vis[x]=1;
ans[col].push_back(x);
for(node i:edge[x])if(mark[i.num]==0) dfs(i.to);
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int x,y;cin>>x>>y;
edge[x].push_back({y,++cnt});
edge[y].push_back({x,cnt});
}
for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i,0);
for(int i=1;i<=n;i++) if(!vis[i]) col++,dfs(i);
cout<<col<<"\n";
for(int i=1;i<=col;i++){
cout<<ans[i].size()<<" ";
for(int j:ans[i]) cout<<j<<" ";
cout<<'\n';
}
}
|
对于根节点,如果他有多于两个儿子,则根节点为割点。
否则:如果一个点有儿子的 $low[to]\ge dfn[x]$ ,那么 $x$ 为割点。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
#include<bits/stdc++.h>
#define pii pair<int,int>
using namespace std;
const int N=2e4+10;
struct node{int to,num;};
vector<node>edge[N];
bool ans[N];
int dfn[N],low[N],n,m,cnt,Time;
void dfs(int x,int fa){
int cnt=0;
dfn[x]=low[x]=++Time;
for(node i:edge[x]){
if(!dfn[i.to]){
dfs(i.to,x);cnt++;
low[x]=min(low[x],low[i.to]);
if(low[i.to]>=dfn[x]&&fa!=0) ans[x]=1;
}else if(i.to!=fa) low[x]=min(low[x],dfn[i.to]);
}
if(!fa&&cnt>=2) ans[x]=1;
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int x,y;cin>>x>>y;
edge[x].push_back({y,++cnt});
edge[y].push_back({x,cnt});
}
for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i,0);
int cnt=0;
for(int i=1;i<=n;i++) if(ans[i]) cnt++;
cout<<cnt<<'\n';
for(int i=1;i<=n;i++) if(ans[i]) cout<<i<<" ";
}
|
对于一个点双,它在 DFS 搜索树中 $dfn$ 值最小的点一定是割点或者树根。
我们用栈维护点,当遍历到某个点时将其入栈。
当某个点是割点或根时,就弹栈直到其儿子被弹出,弹出的这些点都与这个割点或根属于一个点双。
注意特判:根是一个孤立的点没有儿子时,自己是一个点双。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10;
int dfn[N],low[N],n,m,cnt,Time,mark[N],col,vis[N];
struct node{int to,num;};
vector<node>edge[N];
vector<int>ans[N];
stack<int>s;
void tarjan(int x,int frm){
dfn[x]=low[x]=++Time;s.push(x);
for(node i:edge[x]){
if(!dfn[i.to]){
tarjan(i.to,i.num);
low[x]=min(low[x],low[i.to]);
if(low[i.to]>=dfn[x]){//是割点或根
col++;
while(s.top()!=i.to){//弹栈直到儿子
ans[col].push_back(s.top());
s.pop();
}
ans[col].push_back(s.top());
s.pop();//将儿子弹栈,且加入点双
ans[col].push_back(x);//割点也属于点双
}
}else if(i.num!=frm) low[x]=min(low[x],dfn[i.to]);
}
if(!edge[x].size()&&!frm) ans[++col].push_back(x),s.pop();
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int x,y;cin>>x>>y;
if(x==y) continue;
edge[x].push_back({y,++cnt});
edge[y].push_back({x,cnt});
}
for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i,0);
cout<<col<<"\n";
for(int i=1;i<=col;i++){
cout<<ans[i].size()<<" ";
for(int j:ans[i]) cout<<j<<" ";
cout<<'\n';
}
}
|
§在有向图中
Tarjan 用来求强联通分量。
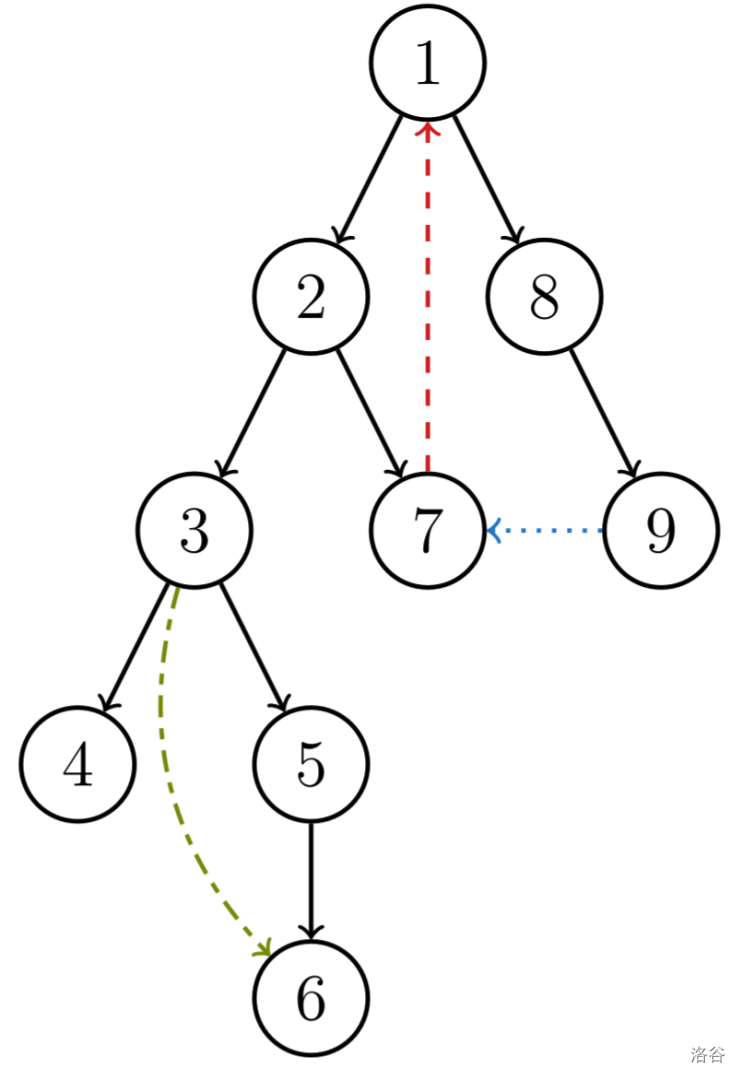
有向图的 DFS 生成树主要有 4 种边(不一定全部出现):
- 树边(tree edge):示意图中以黑色边表示,每次搜索找到一个还没有访问过的结点的时候就形成了一条树边。
- 反祖边(back edge):示意图中以红色边表示(即 $7\to1$),也被叫做回边,即指向祖先结点的边。
- 横叉边(cross edge):示意图中以蓝色边表示(即 $9\to7$),它主要是在搜索的时候遇到了一个已经访问过的结点,但是这个结点 并不是 当前结点的祖先。
- 前向边(forward edge):示意图中以绿色边表示(即 $3\to6$),它是在搜索的时候遇到子树中的结点的时候形成的。
横叉边无效,且干扰算法,通过判断点是否在栈中,判掉。
对于一个连通分量图,在该连通图中有且仅有一个点使得 $dfn[x]=low[x]$ 。该结点一定是在深度遍历的过程中,该连通分量中第一个被访问过的结点,因为它的 $dfn$ 和 $low$ 值最小,不会被该连通分量中的其他结点所影响。
所以,我们每遇见一个 $dfn[x]=low[x]$ 的点,就弹栈直到自己被弹出,这些联通的点构成一个强联通分量。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
#include<bits/stdc++.h>
using namespace std;
const int N=5e5+10;
int dfn[N],low[N],n,m,cnt,Time,mark[N],vis[N],bel[N];
vector<int>edge[N];
stack<int>s;
void tarjan(int x){
dfn[x]=low[x]=++Time;
s.push(x);vis[x]=1;
for(int to:edge[x]){
if(!dfn[to]){
tarjan(to);
low[x]=min(low[x],low[to]);
}else if(vis[to])/*vis为是否在栈中*/ low[x]=min(low[x],dfn[to]);
}
if(low[x]==dfn[x]){
cnt++;
while(s.top()!=x){//弹栈直到自己被弹出
vis[s.top()]=0;
bel[s.top()]=cnt;
s.pop();
}
vis[x]=0;
bel[x]=cnt;
s.pop();
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int x,y;cin>>x>>y;
edge[x].push_back(y);
}
for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i);
}
|
